Kategorie: Klasse 8
Gleichungen
Begriff: „Gleichung“
Zwei Terme, die durch ein Gleichheitszeichen verbunden sind, nennt man Gleichung. Diese können eine oder mehrere Variablen enthalten. Werte für die Variablen, die die Gleichung in eine wahre Aussage überführen, nennt man Lösung der Gleichung. Die Lösungen werden als Lösungsmenge L={Lösung} angegeben. Gleichungen können mehrere Lösungen haben.
Arten von Gleichungen:
Gleichungen werden nach der höchsten Potenz ihrer Variablen unterschieden. So heißen Gleichungen „linear“, wenn als höchste Potenz das x enthalten ist. Gleichungen heißen quadratisch, wenn sie x² als höchste Potenz enthalten, „kubisch“ nennt man sie mit x³.
3x + 4 = 4(x – 9) eine lineare Gleichung mit der höchsten Potenz x als Variable – auch Gleichung 1. Grades genannt
3x² + 7x – 1 = 4 eine quadratische Gleichung – auch Gleichung 2. Grades genannt
5x³ + 125 = x² – 7 eine kubische Gleichung – auch Gleichung 3. Grades genannt
Allgemein gilt also:
Eine Gleichung, die \( x^n \) als höchste Potenz ihrer Variablen enthält, nennt man Gleichung „n-ten Grades„.
Lösung einer Gleichung:
Gleichungen zu lösen bedeutet, den Wert für die Variablen zu finden, bei dem die beiden Terme links und rechts des Gleichheitszeichens den gleichen Termwert besitzen.
Methode 1: Probieren!
Durch spontanes oder systematisches Einsetzen von Werten für die Variable, ist es möglich auf die Lösung der Gleichung zu stoßen. Ein sehr zeitaufwendiges Verfahren, das nur für einfache Gleichungen zu empfehlen ist.
Beispiel:
2x + 1 = 7
| Einsetzen von x =1 | 2 * (1) + 1 = 3 | 3 \( \neq \) 7 | x= 1 ist nicht Lösung! |
| Einsetzen von x= 2 | 2 * (2) + 1 = 5 | 5 \( \neq \) 7 | x= 2 ist nicht Lösung! |
| Einsetzen von x= 3 | 2 * (3) + 1 = 7 | 7 = 7 | x= 3 ist Lösung! |
Methode 2: Isolieren der Variable
Umstellen der Gleichung in die Form „x=“ durch die Anwendung der Äquivalenzumformungen.
Anmerkung! Hier werden nur lineare Gleichungen gelöst!
Äquivalenzumformungen sind:
- Addieren oder Subtrahieren von Zahlen oder Termen auf beiden Seiten der Gleichung
- Multiplizieren oder Dividieren von/mit Zahlen oder Termen auf beiden Seiten der Gleichung
- Quadrieren/potenzieren oder radizieren von beiden Seiten der Gleichung
- Seiten vertauschen (beispielsweise, wenn mehr x „hinten“ stehen… 4x… = 9x… )
Beispiel1:
2x + 1 = 7
| 2x+1 | = | 7 | |-1 | Subtrahiere auf beiden Seiten 1 |
| 2x+1 -1 | = | 7 – 1 | Vereinfache! | |
| 2x | = | 6 | |: 2 | Teile beide Seiten durch 2 |
| \( \frac{2x}{2} \) | = | \( \frac{6}{2} \) | Vereinfache! | |
| x | = | 3 | 3 ist Lösung! | |
| L={3} |
Beispiel 2:
4x – 3 = 9x + 22
| 4x – 3 | = | 9x + 22 | |-1 | Addiere auf beiden Seiten 3 |
| 4x – 3 +3 | = | 9x + 22 +3 | Vereinfache! | |
| 4x | = | 9x + 25 | |: -9x | Subtrahiere 9x auf beiden Seiten |
| 4x – 9x | = | 9x + 25 – 9x | Vereinfache! | |
| -5x | = | 25 | |:(-5) | Teile beide Seiten durch (-5) |
| \( \frac{-5x}{-5} \) | = | \( \frac{25}{-5} \) | ||
| x | = | -5 | -5 ist Lösung! Negative Lösung! | |
| L={-5} |
Hier sieht man, wieder wie der 1. Befehl dafür sorgt, dass die -3 „verschwindet“, genau so passiert es mit dem 9x. Durch diese Schrittfolge erreicht man es, dass die Termteile mit der Variable „links stehen“ und die Konstanten (einfache Zahlen) auf der rechten Seite erscheinen.
Strategie für das Lösen von linearen Gleichungen:
- Fasse die Terme beider Seiten so weit wie möglich zusammen!
- Addiere oder subtrahiere geschickt so, dass die „Termteile mit Variable“ (4x , – 7x …) auf der linken Seite stehen!
- Addiere oder subtrahiere geschickt so, dass die Konstanten ( Zahlen: 14 , – 9 oder 3,7) auf der rechten Seite stehen!
- Nun sollte die Gleichung die Form 12x = 27 haben.
- Dividiere beide Seiten durch die Zahl vor der Variable! ( 12x = 27 | :12 )
- Notiere die Lösung! (x=…)
Hier ein paar Beispiele zum Vertiefen!
Achtung! Herr Mathe im Video ist manchmal etwas schnell und inkonsequent…
![]()
Terme – Ausmultiplizieren
Geometrische Deutung:

Der Malpunkt vor der Klammer darf weggelassen werden.
![]()
Maßstäbe
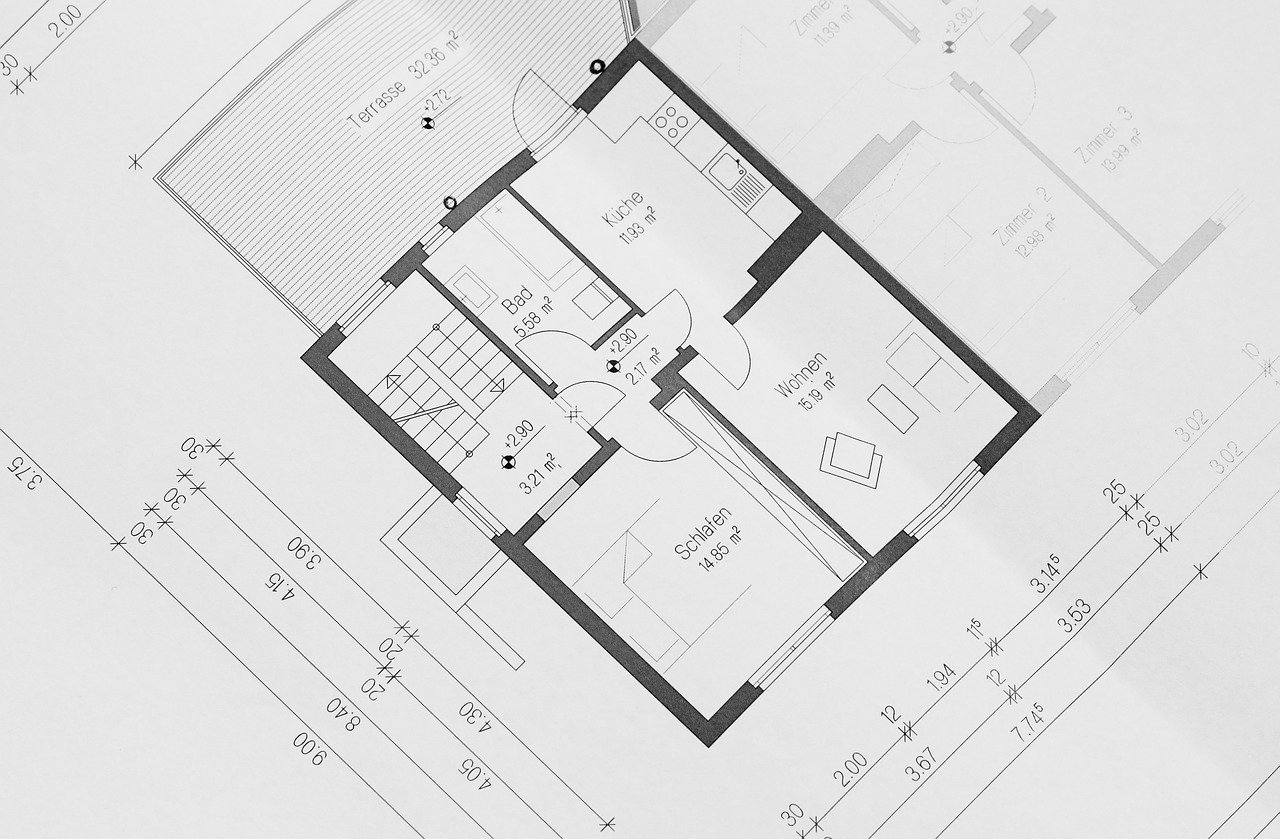
Wir erstellen Modelle, um uns die Details besser zu veranschaulichen. Einige Modelle entstehen durch Vergrößern, andere durch Verkleinern. Im Folgenden findest Du Beispiele für unsere Kreativität.
Besprecht, in welchen Fällen wir die Wirklichkeit vergrößern und in welchen Fällen wir sie verkleinern!
Der Maßstab ist das Verhältnis, in dem diese Darstellung passiert.
Er ist definiert als das:
Verhältnis einer Länge auf der Karte zu ihrer Entsprechung in der Natur.

Wenn du weißt, welche Darstellung benutzt wurde, hast du schon gewonnen. Denn Du wirst immer Aufgaben gestellt bekommen, in denen nur eine der 4 Größen der Gleichungen fehlt.
Anleitung:
Hier geht es immer um Aufgaben mit 3 gegebenen Größen für die Gleichung:
1. Finde die gegebenen Größen!
2. Sorge für Einheitengleichheit! (Bei mehreren Einheiten)
3. Füge die gegebenen Größe in die richtige Gleichung ein und stelle die Gleichung nach der gesuchten Größe um!
Beispiele:
Aufgabe 1:
Herr Meier möchte einen Plan von seinem Haus zeichnen. Er weiß, dass sein Wohnzimmer 7m lang ist und der Plan einen Maßstab von 1:100 haben soll. Wie lang muss das Wohnzimmer in seinem Plan sein?
Finde die gegebenen Größen!
gegeben:
Zeichnung Haus (Verkleinerung)
Maßstab 1 : 100
7m Wohnzimmerlänge (Originalmaß)
Sorge für Einheitengleichheit!
Hier unnötig! Die Einheit ist nur Meter!
Füge die gegebenen Größe in die richtige Gleichung ein und stelle die Gleichung nach der gesuchten Größe um!
Verkleinerung, also …
\( \frac{1}{k} = \frac{Bildmaß}{Originalmaß} \)
Einsetzen der Größen:
\( \frac{1}{100} = \frac{Bildmaß}{7m} | \cdot 7m \)
Isolieren der gesuchten Größe … Die Angabe „7m“ im Nenner stört…
Also,… multiplizieren beider Seiten mit 7m
\( \frac{7m}{100} = Bildmaß \)
\( 0,07m = Bildmaß = 7cm \)
Antwortsatz:
Die Länge des Wohnzimmers auf der Zeichnung beträgt 7cm.
Aufgabe 2:
Welche Höhe hat ein Hochofen, wenn sein Modell im Maßstab 1:2000 nur 32mm hoch ist?
Finde die gegebenen Größen!
gegeben:
Modell Hochofen (Verkleinerung)
Maßstab 1 : 2000
32mm Höhe des Modells (Bildmaß)
Verkleinerung, also …
\( \frac{1}{k} = \frac{Bildmaß}{Originalmaß} \)
Einsetzen der Größen:
\( \frac{1}{2000} = \frac{32mm}{Originalmaß} \)
Die gesuchte Größe steht unten!
Auf beiden Seiten der Gleichung muss der Kehrwert gebildet werden! (Reziprok bilden!)
\( \frac{2000}{1} = \frac{Originalmaß}{32mm} | \cdot 32mm\)
Isolieren der gesuchten Größe … Die Angabe „32mm“ im Nenner stört…
Also,… multiplizieren beider Seiten mit 32mm
\( 32mm \cdot 2000 = Originalmaß \)
\( 64.000mm = Originalmaß = 64m \)
Antwortsatz:
Die Hochofenhöhe beträgt in der Wirklichkeit 64m.
Weiterüben bei aufgabenfuchs.de! Besser werden!
![]()