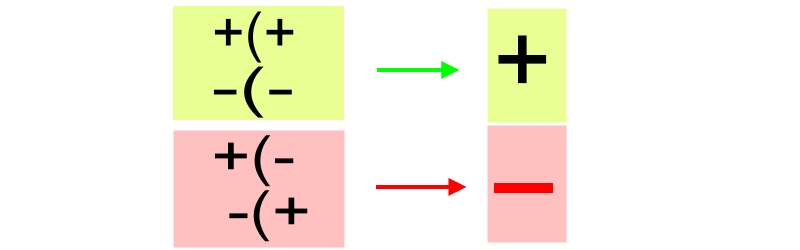
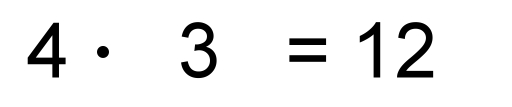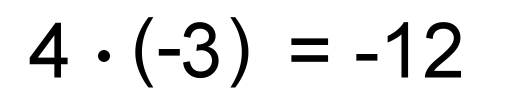Die Zahlenbereiche
Zuerst lernen wir zählen!
Nicht sofort mit Null beginnend aber fortlaufend zählten wir stolz … 1, 2, 3, 4, 5, 6 und so weiter.
Dass zwischen den Zahlen „Lücken“ bestehen, ist uns anfangs nicht bewusst. Schnell merkt man jedoch bei der Angabe von Geld oder Zeiten, Weiten und Höhen im Sport, dass da noch mehr sein muss.
Ein Wechselgeld von 3,07€ oder unsere Höchstleistung beim Weitsprung mit 2,47m zeigen das.
Zur Unterscheidung der Zahlenarten kann man sich die Zahlen als Mengen vorstellen.
So enthält die Menge aller natürlichen Zahlen( \(\Bbb N \) ) die Null als kleinste Zahl und alle folgenden Zahlen mit dem jeweiligen Abstand Eins voneinander.
( \(\Bbb N \) )={0,1,2,3,4,5,6,7,8,9…}
Die Null – und alle anderen natürlichen Zahlen – gehört allerdings auch zu den gebrochenen Zahlen ( \(\Bbb Q + \) ), also den positiven Brüchen. Das Mengendiagramm zeigt dieses Verhältnis. Zahlenmengen werden oft als Ellipsen veranschaulicht.

Man schreibt:
\(\Bbb N \) < \(\Bbb Q + \) oder besser \(\Bbb N \subset \Bbb Q + \)
Da es gebrochene Zahlen( \( \frac{3}{4} \) oder 0,72 ) gibt, die keine natürlichen Zahlen sind, muss die Menger der gebrochenen Zahlen größer sein, als die Menge der natürlichen Zahlen.
Die Menge der natürlichen Zahlen ist eine Teilmenge der gebrochenen Zahlen \(\Bbb N \subset \Bbb Q + \)
Weitere Zahlenbereiche sind beispielsweise die rationalen Zahlen \(\Bbb Q \), die ganzen Zahlen ( \(\Bbb Z \) ) und die reellen Zahlen ( \(\Bbb R \) ).
Eine gute Übersicht dazu findest du hier.
Und hier noch als Video …
![]()