Durch Bewegungen wie Drehung, Spiegelung und Verschiebung in Kombination mit dem maßstäblichen Vergrößern oder Verkleinern entstehen zueinander ähnliche Figuren.

„Figur 1 ist ähnlich zur Figur 2.“ Man schreibt: F1 ~ F2

Bring das grüne Fünfeck durch Strecken(k) (maßstäbliches Vergrößern oder Verkleinern) und das Spiegeln (Spiegle) zur Deckungsgleichheit (Kongruenz). Gelingt dies, so waren die Ausgangsflächen zueinander ähnlich. Am roten Eckpunkt lässt sich die Figur auch frei Verschieben.

Gelingt das auch hier?

Versuche, das grüne A durch Strecken(k) (maßstäbliches Vergrößern oder Verkleinern) und das Spiegeln (Spiegle) zur Deckungsgleichheit (Kongruenz) mit dem blauen A zu bringen. Gelingt dies nicht, so waren die Ausgangsflächen zueinander nicht ähnlich. Am roten Eckpunkt lässt sich die Figur auch frei Verschieben.

„Figur 1 ist nicht ähnlich zur Figur 2.“ Man schreibt: F1 ≁ F2

Hinter der Idee des Streckens steckt die „zentrische Streckung„

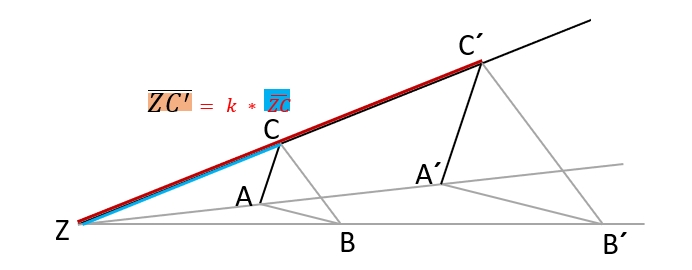
Von einem Streckungszentrum Z werden Strahlen zu allen Eckpunkte einer Original-Figur gezeichnet. Auf diesen Strahlen werden die Abstände zwischen Zentrum Z und Originalfigur-Eckpunkten (A,B,C) entsprechend des Streckungsfaktors k vervielfacht abgetragen. Es entstehen die Strecken \( \overline{ZA‘}, \overline{ZB‘}, \overline{ZC‘} \) .

Es gilt: \( \overline{ZA‘} \) = \( k * \overline{ZA} \) ; \( \overline{ZB‘} \) = \( k * \overline{ZB} \) ; \( \overline{ZC‘} \) = \( k * \overline{ZC} \)

Weitere Erklärhilfen: