Winkelbegriff – Bogenmaß – Übung

Ordne die Winkel innen an und die Vielfachen von \( /Pi \) außen an.
liveworksheets.com
![]()
Mathe muss man üben!


Ordne die Winkel innen an und die Vielfachen von \( /Pi \) außen an.
![]()
Für diese Lektion solltest Du unbedingt die Umstellung von Formeln und Gleichungen beherrschen!
Im Dreieck liegt dem kleinsten Winkel die kürzeste Seite gegenüber.
Dem größten Winkel liegt die längste Seite gegenüber!
Im rechtwinkligen Dreieck gibt es 2 spitze Winkel.
Für diese spitzen Winkel gilt:
Ein Schenkel des Winkels ist die Hypotenuse des Dreiecks.
Der andere Schenkel wird Ankathete (AK) des Winkles genannt!
Die dem Winkel gegenüberliegende Seite ist eine Kathete. Sie wird Gegenkathete (GK) des Winkels genannt!


Für die Größen am rechtwinkligen Dreieck gelten folgende Beziehungen und Rechenvorschriften!
Wenn x ein spitzer Winkel des rechtwinkligen Dreiecks ist:

Zwei der Größen einer dieser obigen Gleichungen müssen bekannt sein,
um die dritte Größe in dieser Gleichung zu berechnen!
Beispiel Winkelberechnung:
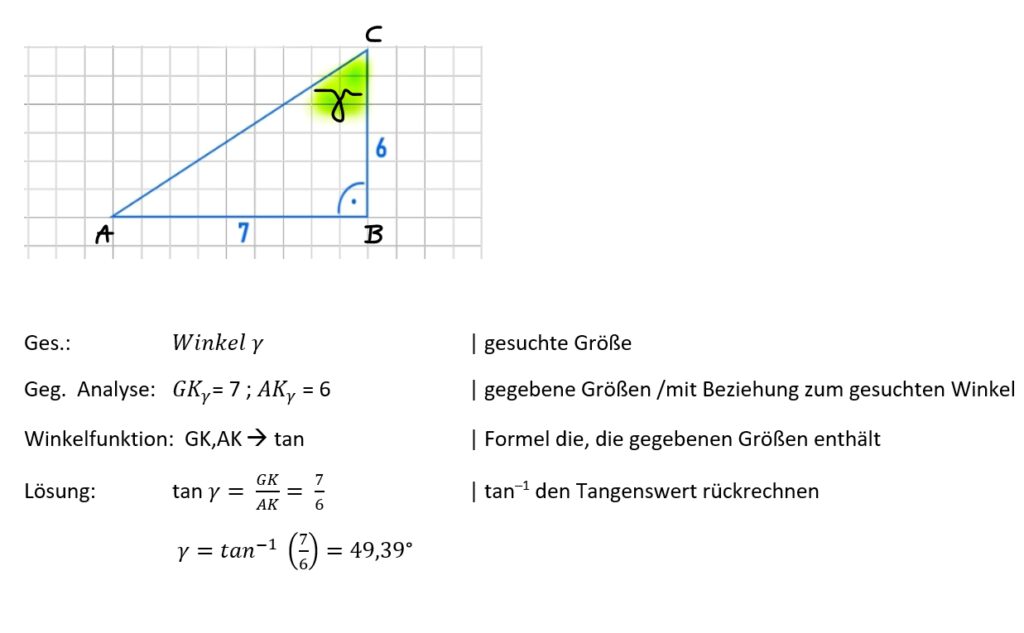
![]()
In einem rechtwinkligen Dreieck ist die Seite gegenüber dem rechten Winkel die längste Seite des Dreiecks.
Sie wird Hypotenuse genannt.
Die beiden kürzeren Seiten nennt man Katheten, sie sind die Schenkel des rechten Winkels.

Auch in den anderen Lagen bleibt diese Relation erhalten! Der rechte Winkel bestimmt die Funktion der Seiten!

Der griechische Mathematiker und Philosoph Pythagoras von Samos entdeckte einen fundamentalen Zusammenhang zwischen Hypothenuse und den Katheten. Bis heute ist dies eine der wichtigsten Erkenntnisse der Mathematik!
Wir im obigen Video zu sehen ist, füllen die beiden Quadrate der Katheten (a , b )
zusammen das Quadrat der Hypotenuse (c) .
Man schreibt:
a² + b ²= c²
Der berühmte Satz des Pythagoras!
Die Summe der Quadrate der Katheten ist gleich dem Quadrat der Hypotenuse!

Dieser Zusammenhang ermöglicht uns bei 2 bekannten Seiten
eines rechtwinkligen Dreiecks die Berechnung der 3. Seite!
Beweis des Satzes des Pythagoras!
Beispiel: Berechnung einer Hypotenuse!

Beispiel: Berechnung einer Kathete!

![]()

Die im ersten Schritt eingezeichnete Höhe zur Seite c \( (h_c) \) kann auch als \( a*sin\beta \) betrachtet werden, da sie durch \( sin\beta= \frac{Gegenkathete}{Hypotenuse} \) also hier \( sin\beta= \frac{h_c}{a} \) festgelegt ist. Analog gilt das auch für \( a*cos\beta\).
Autor: just01120, Martin Zeindl, geogebra.org
![]()