Winkel am Einheitskreis (Kreativ)

Verändere mit dem Schieberegler den Winkel so, dass er dem geforderten Vielfachen der Kreiszahl entspricht.
Für die Erzeugung negativer Winkel nutze „Switch Direction“.
Autor: Tim Brzezinski, geogebra.org
![]()
Mathe muss man üben!


Verändere mit dem Schieberegler den Winkel so, dass er dem geforderten Vielfachen der Kreiszahl entspricht.
Für die Erzeugung negativer Winkel nutze „Switch Direction“.
Autor: Tim Brzezinski, geogebra.org
![]()

![]()
Die Funktion y = a *sin (x)
Der Faktor a bewirkt eine Vervielfachung der Funktionswerte, wie wir sie schon von anderen Funktionen her kennen.
Sein Effekt auf den Graphen nennt man Streckung für a>1 und Stauchung für 0<a< 1.
Funktionswerte verkleinern / vergrößern sich, das Maximum/ Minimum liegt dann bei a und -a und nicht mehr bei 1 und -1.
Die „Lage der Nullstellen“ und die „Länge der kleinsten Periode“ beeinflusst der Koeffizient a nicht.
Nutzt man negative Werte für a, kommt es zur Spiegelung des Graphen an der x-Achse(Abszisse).
Die Amplitude – die Ausschlaghöhe – der Funktion wird hier beeinflusst.
Probiere hier aus, wie der Koeffizient a auf den Graphen wirkt!
Quelle: Christian Bauer , geogebra.org
Die Funktion y = sin (bx)
Der Faktor b führt bei bei der Funktion zur Veränderung der kleinsten Periode.
Normalerweise beträgt sie bei y=sin(x) genau 2![]() .
.
Der Faktor b verändert diese Länge auf der x-Achse, auf der sich der Graph periodisch wiederholt.
Die Periodenlänge errechnet sich aus:
$$\frac {2* \pi}{b} $$
Das Intervall von Null bis zum Wert der kleinsten Periode sollte dann zur Zeichnung geviertelt werden, um
Maxima, Minimum und Nullstellen zu errechnen.
Untersuche den Einfluss von b auf den Graphen von y = sin (b*x)
Quelle: Christian Bauer, geogebra.org
Beide Faktoren in der Funktion y=f(x) = \( a \cdot sin(b \cdot x \) )
Zeichnen von Funktionen dieser Form:
(1) Sollte a<0 sein, so tauschen \( y_{max} , \) und \( y_{min} , \) die Funktion
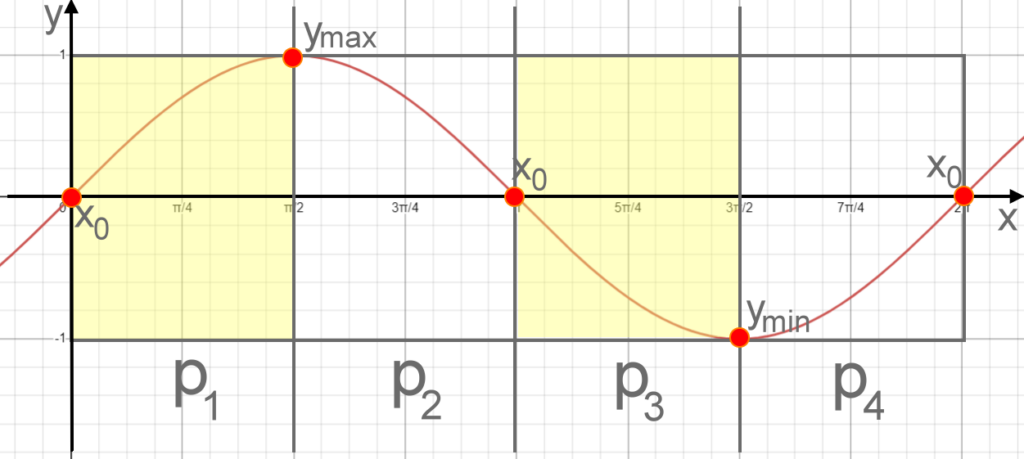
Beispiel: y=f(x) =3 sin (2x); a = 3; b = 2
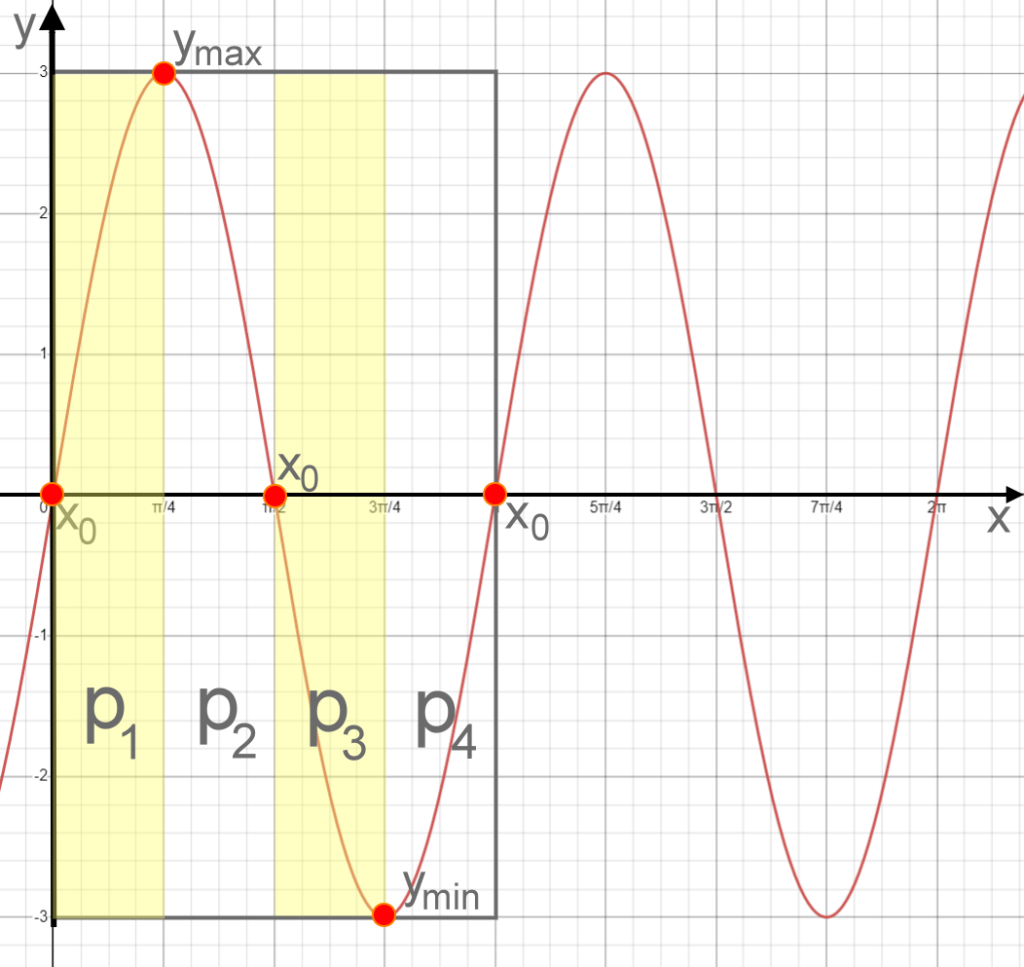
Eventuell sollten bei großen Werten für a oder b auch Wertetabellen zum Einsatz kommen, die das harmonische Zeichnen mit Zwischenwerten unterstützen.
Die Funktion y=f(x)=a sin (bx) + c (mit Physik – Fachsprache)
![]()
Zeichne einen Kreis in ein Koordinatensystem mit dem Radius 1 und dem Mittelpunkt im Ursprung des Systems.

Festlegung:
Dieser Kreis hat den Radius r=1.
Sein Umfang beträgt u= ![]() * d = 2
* d = 2![]()
Der Umfang des halben Kreises beträgt somit ![]() .
.
Die Länge der Peripherielinie (b), die zu einem Winkel gehört, wird Bogenmaß (b) genannt.

Bezogen auf den Umfang des Kreises bilden sich Wertepaare (\( \alpha \) , b)
| Winkel \( \alpha \) | Bogenmaß b |
| 0° | 0* |
| 30° | |
| 60° |  /3 /3 |
| 90° |  /2 /2 |
| 180° |  |
| 270° | 3 /2 /2 |
| 360° | 2 |
Die Umrechnung Winkel – Bogenmaß
Mit Hilfe der unten stehenden Formel, die man auch in jedem guten Tafelwerk findet, kann man Winkelmaß in Bogenmaße umwandeln und umgekehrt.
$$b= \frac {\alpha}{360°} *2\pi $$
Winkel und Bogenmaß im Taschenrechner
Unser Taschenrechner rechnet in der Voreinstellung mit Winkeln im Vollkreis von 360° DEG (..von Degree)
Mit dem Bogenmaß kann unser Taschenrechner auch rechnen. Dazu stellt man im Setup auf RAD (…Radiant) um.
Damit ist es nun auch möglich, die Sinus-Funktion unabhängig von der Winkelangabe im Koordinatensystem aufzutragen. Man erstellt eine Wertetabelle für y = f(b) = sin(b) , wobei nur noch reelle Zahlen benötigt werden. Das b wird durch x ersetzt und wir
können wie bei Funktionen gewohnt schreiben:
$$ y = f(x) = sin (x) ; x\in R $$
Nun sind jedoch Werte der x-Achse wie 1 oder 2 oder 3 uninteressant, denn die Teile und Vielfachen von ![]() bestimmen das Aussehen und die Eigenschaften von y = sin (x)
bestimmen das Aussehen und die Eigenschaften von y = sin (x)
[weiterarbeiten…]
Damit wird die sehr unübersichtliche Darstellung von Winkeln auf der x-Achse überflüssig!
VIDEO Sinus-Funktion im Koordinatensystem
Sehr schöne Animation zur Darstellung Winkel –> sin(Winkel)
https://www.matheretter.de/do/loadprog?id=115
Mit der Hypotenuse r=1 ergeben sich die Längen der Katheten als \( cos \alpha \) und \( sin \alpha \) .
![]()