Die Exponentialfunktion
Das Koli-Bakterium (Escherichia coli)
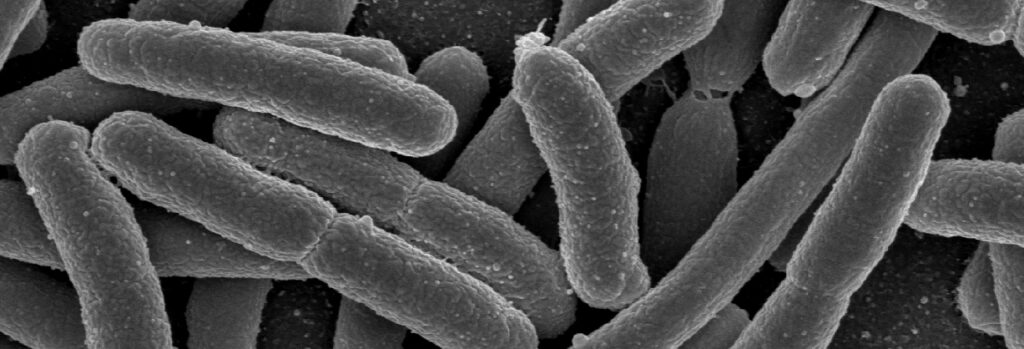
Bakterien vermehren sich durch Spaltung(Mitose) . Dies geschieht in gleichen Zeitabständen. Die Zeit zur Verdopplung der Bakterienpopulation nennt man Generationszeit. Die Generationszeit der Kolibakterien (sh. Abbildung) im Darmtrakt von Warmblütern also auch in unserem Darm beträgt beispielsweise 20min. Unser Stuhl enthält bis zu \( 10^9 \) (1 Mrd.) dieser Keime pro Gramm. Gelangen diese Keime jedoch in die Blase, kann das zu Erkrankungen durch Entzündungen führen. Eine fahrlässige Aufnahme kann also negative Folgen haben. Wasser sollte man daher aus kontrollierten Beständen trinken oder abkochen, denn das tötet die Keime.
Badegewässer von „guter Qualität“ dürfen bis zu 1000 koloniebildende Einheiten(CFU) pro 100ml Wasser enthalten.
Beachte: Eine Verdopplung dieser Keime findet alle 20 Minuten statt!
Nehmen wir eine Probe und untersuchen den Anstieg der Keimzahl.
| Zeit (in Minuten) | 0 | 20 | 40 | 60 | 80 | 100 | 120 |
| Keimzahl | 1.000.000 | 2.000.000 | 4.000.000 | 8.000.000 | 16.000.000 | 32.000.000 | 64.000.000 |
Die Keimzahl hat sich nach einer Stunde verachtfacht. Nach 2 Stunden jedoch hat sie sich bereits auf das 64-fache vergrößert! Nach 3 Stunden(9 Verdopplungen also ) ist die Probe dann auf das 512-fache oder \( (2^9 -fache) \) angestiegen!
Aufgabe: Stelle die Daten in einem Koordinatensystem dar, um den graphischen Verlauf zu sehen. (Lösungsbild)
Wächst eine Größe in gleichen Zeitabschnitten immer um den gleichen Faktor, so spricht man von exponentiellem Wachstum.
(Verkleinert sich eine Größe in gleichen Zeitabständen derart , so spricht man von exponentiellem Zerfall.)
| Zeit (in Minuten) | 0 | 20 | 40 | 60 | 80 | 100 | 120 |
| Keimzahl | 1.000.000 | 2.000.000 | 4.000.000 | 8.000.000 | 16.000.000 | 32.000.000 | 64.000.000 |
| Wachstum a | —►*2 a=2 | —►*2 a=2 | —►*2 a=2 | —►*2 a=2 | — ►*2 a=2 | —►*2 a=2 | —►*2 a=2 |
| n=0 \( K_0 \) | n=1 \( K_1 \) | n=2 \( K_2 \) | n=3 \( K_3 \) | n=4 \( K_4 \) | n=5 \( K_5 \) | n=6 \( K_6 \) |

Ebenso wie das Wachstum von Zellkulturen verhalten sich auch andere Naturphänomene:
- der radioaktive Zerfall
- der Luftdruckverlauf in der Atmosphäre
- die Erwärmung oder Abkühlung von Körpern
- Ladungskurven elektrischer Kondensatoren
- Entleeren eines Wasserbehälters (Auslass unten)
- katalytischer Abbau von Stoffen bei chemischen Reaktionen
Die Wasserhyazinthen – erst gewollt, nun gehasst
Als Zierpflanze zur Verschönerung der Gartenteiche gelangte die wild wuchernde Pflanze in die ganze Welt. Die eigentlich nur in Südamerika wachsende Wasserpflanze hatte seit dem 18. Jahrhundert auch in Afrika eine neue Heimat gefunden. Ohne Fressfeinde vermehrt sich die Schwimmpflanze massenhaft und wuchert sämtliche Binnengewässer in Afrika zu. Eine Wasserhyazinthen-Decke verdoppelt ihre Fläche in nur zwei Wochen. Durch den Lichtmangel unter den Pflanzenteppichen sterben die beheimateten Wasserpflanzen ab und auch die Fische sterben als Folge. Außerdem behindern die dicken Schwimmpflanzenteppiche die Schifffahrt und Fischerei. Die Folgen für das Ökosystem sind verheerend. Doch nach jahrelangen Bekämpfungsversuchen, gibt es nun Abhilfe – durch gefräßige Insekten.
Die dickstielige Wasserhyazinthe wurde im Jahr 2016 in die „Liste der unerwünschten Arten“ für die Europäische Union aufgenommen.
(Textauszüge aus: https://de.wikipedia.org/wiki/Dickstielige_Wasserhyazinthe)
Funktionen der Form y=f(x)=\( c \cdot a^{x} \) mit a>0 und a≠1 nennt man Exponentialfunktionen. Die Variable x übernimmt hier die Funktion des Exponenten einer Potenz in der Funktionsvorschrift.
| Definitionsbereich: | Wertebereich | besondere Punkte | Nullstellen |
| \( x \in \mathbb{R} \) | \( (0 ; \infty) \) | (0|c) (1| \( c \cdot a \) ) | keine Nullstellen |
Damit ist aus dem Graphen der Funktion der Anfangswert c direkt als Schnittpunkt des Graphen mit der y-Achse (Ordinate) ablesbar. Der Punkt (1|y) liefert dann den Wachstumsfaktor a aus der Rechnung a = \( \frac{y}{c} \).
Für Werte a > 1 entstehen monoton steigende Graphen, die exponentielles Wachstum darstellen.
Für Werte 0 < a < 1 zeigen die entstehenden Graphen exponentiellen Zerfall (negatives Wachstum) an.
Quelle: geogebra.org, Tanja Wassermair
Die Skalierung der y-Achse ist hier eine wichtige Vorbereitung zur Darstellung dieser Funktionen, deshalb ist \( y_{max} \) des gewünschten Wertebereichs eine wichtige Größe. Die x-Achse wird an den Wachstumszyklus (Wachstumsintervall) angepasst. Eine 1:1 Skalierung der Achsen des Koordinatensystems ist also bei der Darstellung von Exponentialfunktionen nur selten sinnvoll.
Beispiele und Illustrationen
►(Gegenüberstellung Wachstum/Zerfall bei desmos.com)
►Darstellung Wachstum mit Wertetabelle
►(Darstellung Zerfall, Illustration mit Wertetabelle)
![]()
