Flächen – Rückschlussrechnung (Formeln umstellen)
![]()
Gib die Lösung mit Einheit an und setze zwischen Zahl und Einheit ein Leerzeichen!
![]()
Mathe muss man üben!

![]()
Gib die Lösung mit Einheit an und setze zwischen Zahl und Einheit ein Leerzeichen!
![]()
![]()
![]()
Du hast über die Schuljahre die wichtigsten Standardflächen (Rechteck, Kreis,…)kennengelernt und erkennst diese an ihren Eigenschaften. Ihre Kennlinien (Seiten, Diagonalen, Höhen, Winkel) nutzt du zur Flächen- und Umfangsberechnung. Dabei hast du gelernt, dass Skizzen gute Helfer sind und Benennungen und Bemaßungen Übersichtlichkeit schaffen.
Mit der folgenden Strategie zur Flächenberechnung sollten sich die meisten Aufgaben lösen lassen:

Die Dreiecksberechnung (Trigonometrie) bildet den Abschluss der Flächenberechnung an der Oberschule. Hier musst du dein gesamtes Können anwenden um auch die komplexen Aufgaben zu meistern, die am allgemeinen Dreieck gestellt werden.
Strategie Dreiecksberechnung:
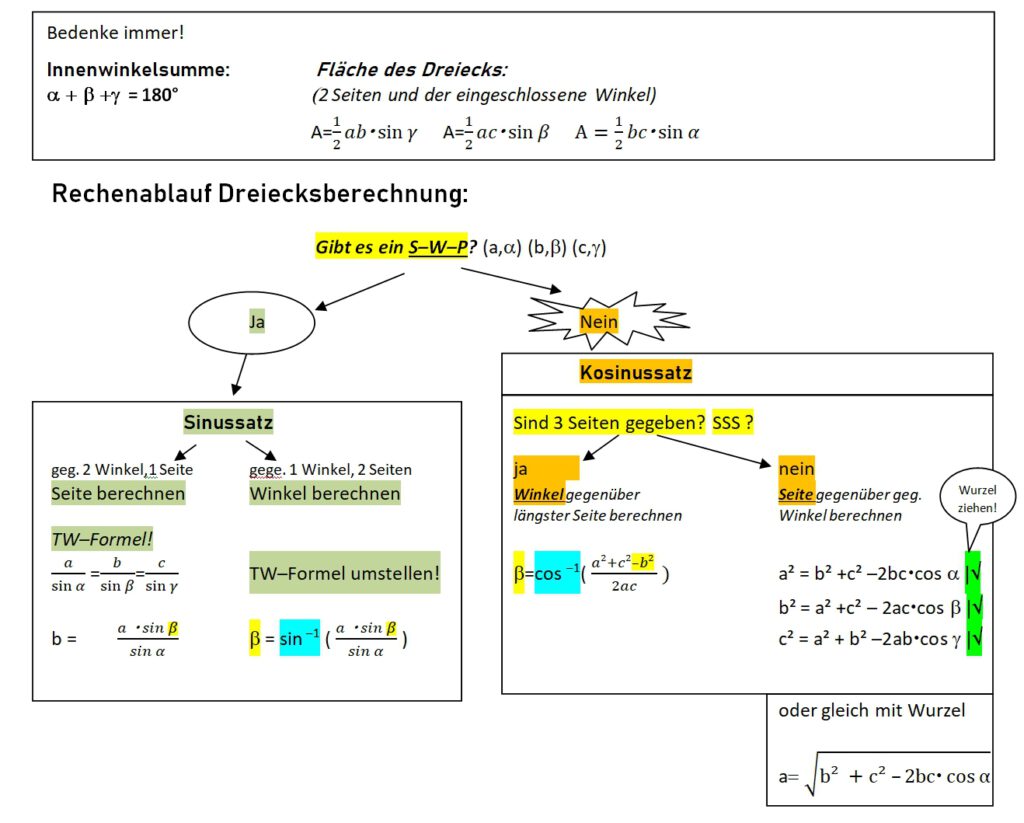
![]()
![]()
Quelle: sozpaed, www.geogebra.org
![]()