Mathe muss man üben!
Die drei Innenwinkel im Dreieck summieren sich immer zu 180°.
$$ \alpha + \beta + \gamma = 180° $$
Mach ein Experiment:
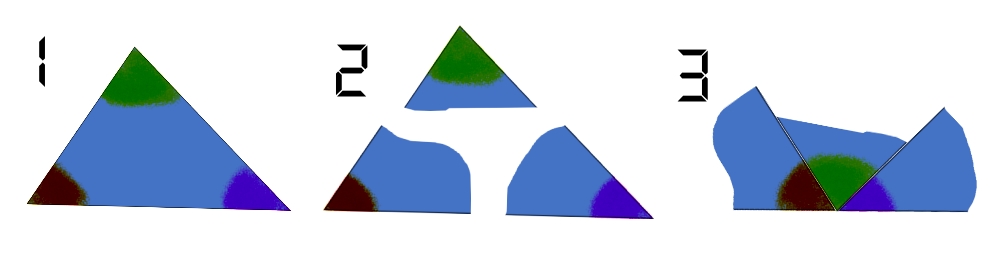
Oder vertraue den Zahlen…
Probiere es hier aus…rechne nach!
Das Trapez ist ein Viereck mit 2 parallelen Seiten.
Die Formeln in Tafelwerken beziehen sich nur auf Trapeze mit den Parallelen a und c also a||c.
Daher ist es dringend notwendig, die Formeln und Gleichungen auf das eigene Trapez anzupassen.
Am Trapez gibt es normalerweise keine gleich großen Winkel. Jedoch stehen die Winkel paarweise durch die Lage an verschiedenen Parallelen in einer Beziehung.
Man sieht, dass die Winkelpaare jeweils in Nebenwinkelbeziehungen stehen. Nebenwinkel ergänzen sich zu 180°.
Am gleichschenkligen oder symmetrischen Trapez gelten noch zusätzliche Winkelbeziehungen:
Für die Berechnung der Fläche und für die Konstruktion des Trapezes ist es nötig, die Trapezhöhe zu kennen.
Die Trapez-Höhe ist die senkrechte Verbindung zwischen den Parallelen!
Wo man die senkrechte Verbindung zwischen den Parallelen zeichnet ist dabei egal.
weiter zu :
Berechnen an Trapezen– Fläche und Umfang
…einfach erklärt von Lehrer Schmidt
und noch mal mit Erklärungen zu den verwendeten Formeln :
Das Drachenviereck ist achsensymmetrisch mit einer Symmetrieachse (hier e) . Seine Diagonalen (e,f) stehen senkrecht aufeinander und die Symmetrieachse halbiert die andere Diagonale. Die beiden Winkel, deren Scheitelpunkte nicht an der Symmetrieachse liegen, sind gleich groß.
Der Flächeninhalt eines Drachenvierecks/Deltoids
Konstruktion:
Konstruktion und Berechnung: