Die quadratische Funktion y=x²
Die quadratische Funktion y=x²
Die Funktion y=x² besitzt einen achsensymmetrischen Graphen, der den Scheitelpunkt (0|0) besitzt. Die Nullstelle der Funktion liegt ebenfalls bei (0|0) im Koordinatenursprung.
Die Funktion fällt im Intervall (-∞ ; 0 ) und steigt im Intervall (0 ; ∞).
Die Wertetabelle:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y=x² | (-3)*(-3) = 9 | (-2)*(-2) = 4 | (-1)*(-1)=1 | 0*0= 0 | 1*1=1 | 2*2=4 | 3*3=9 |
Der Graph der Funktion im Intervall (-2,8 ; 2,8)
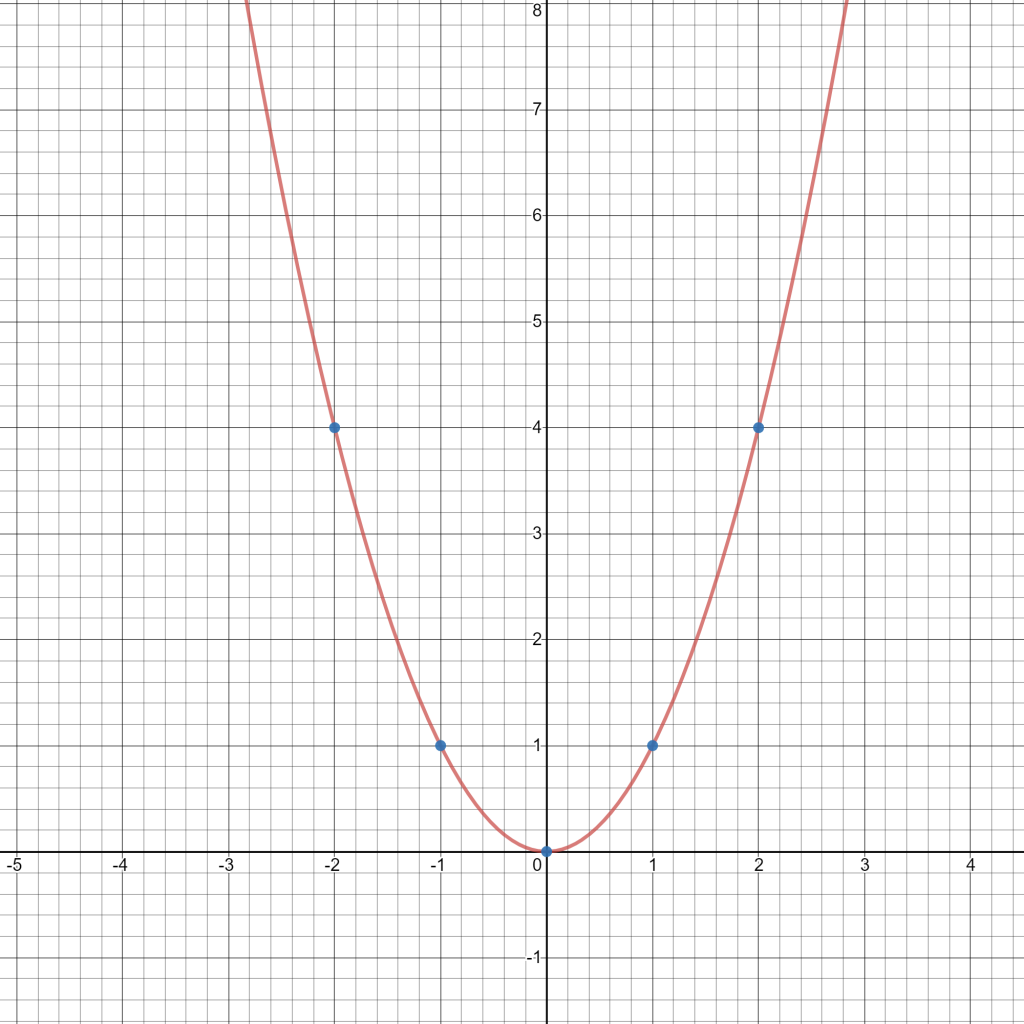
Bearbeite die Funktion bei www.desmos.com
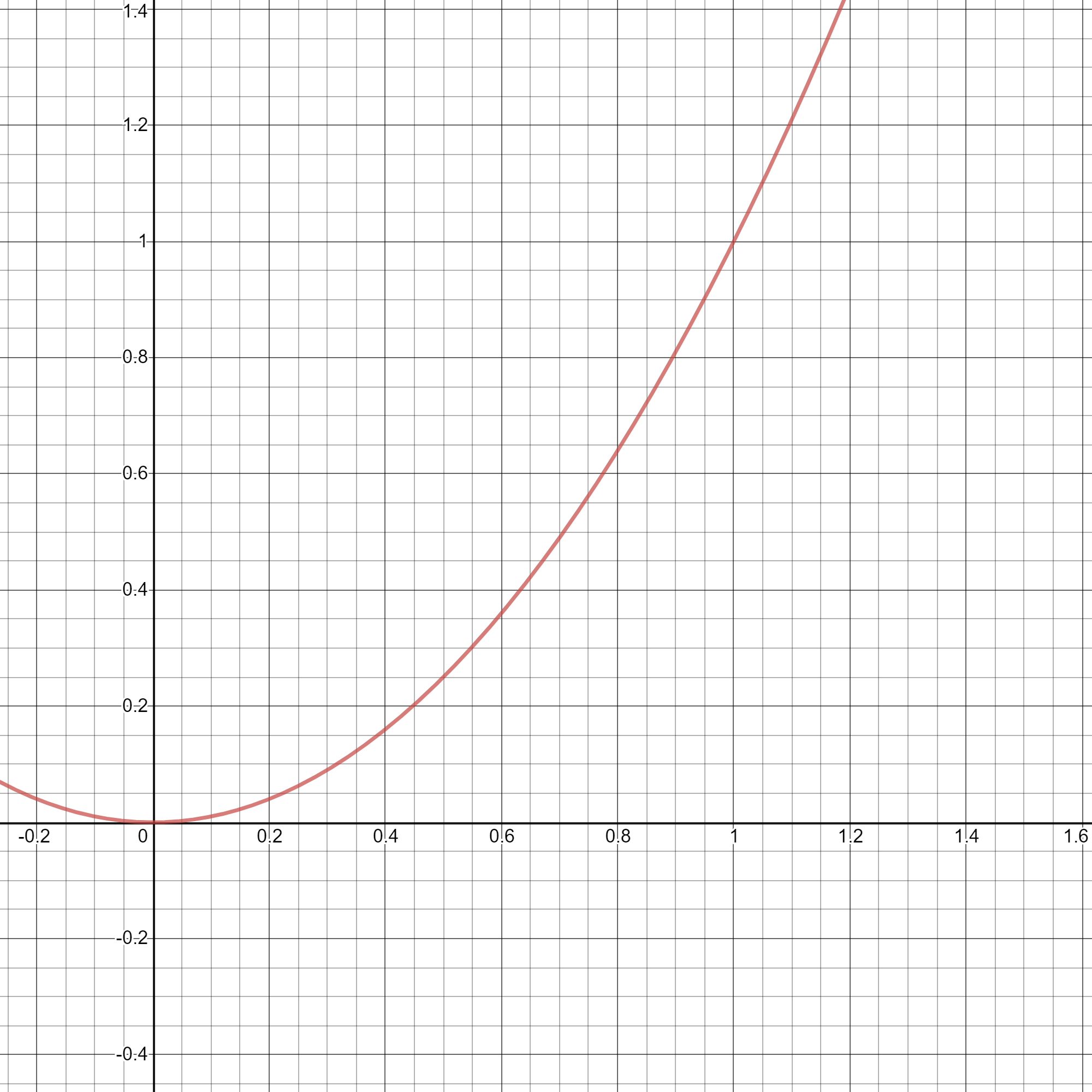
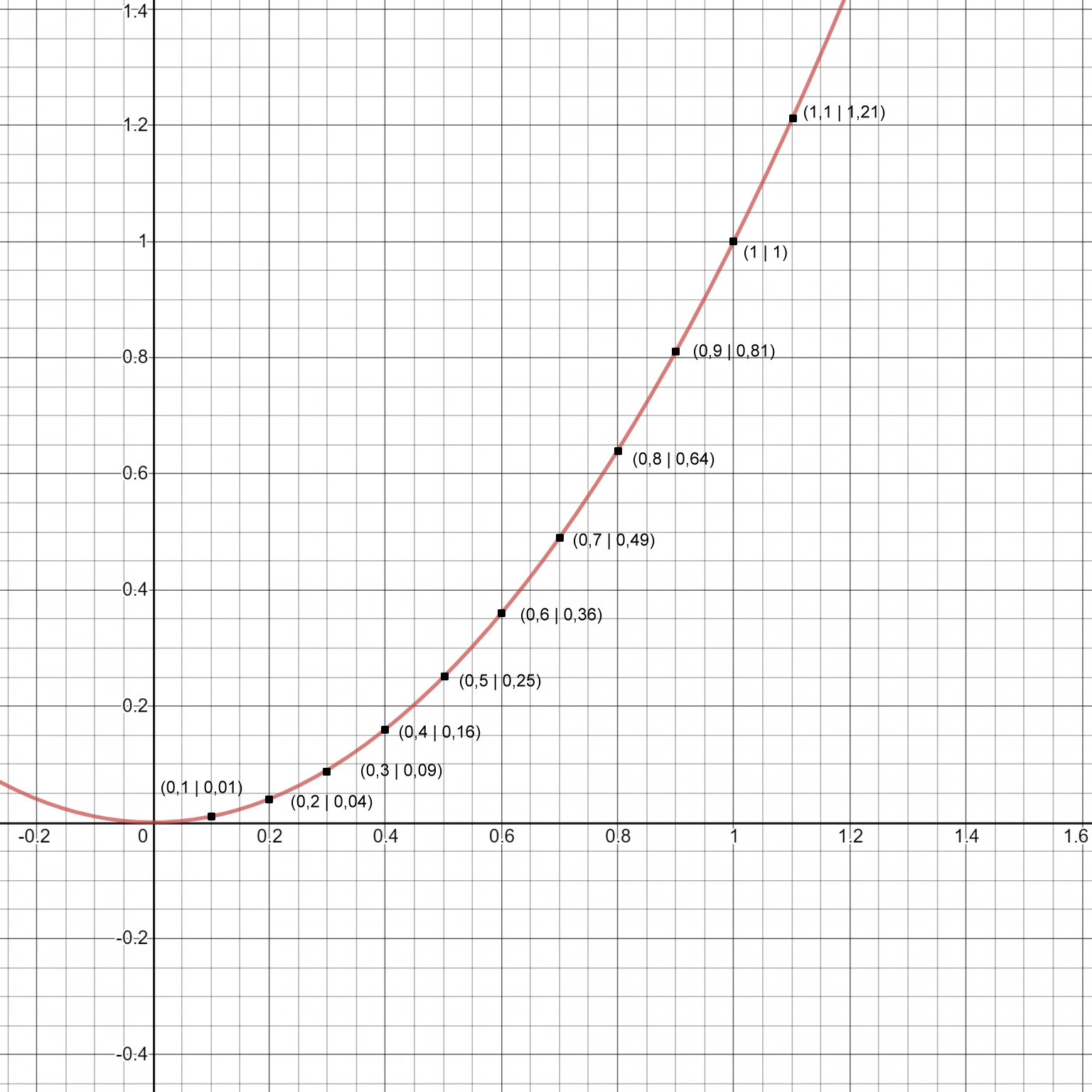
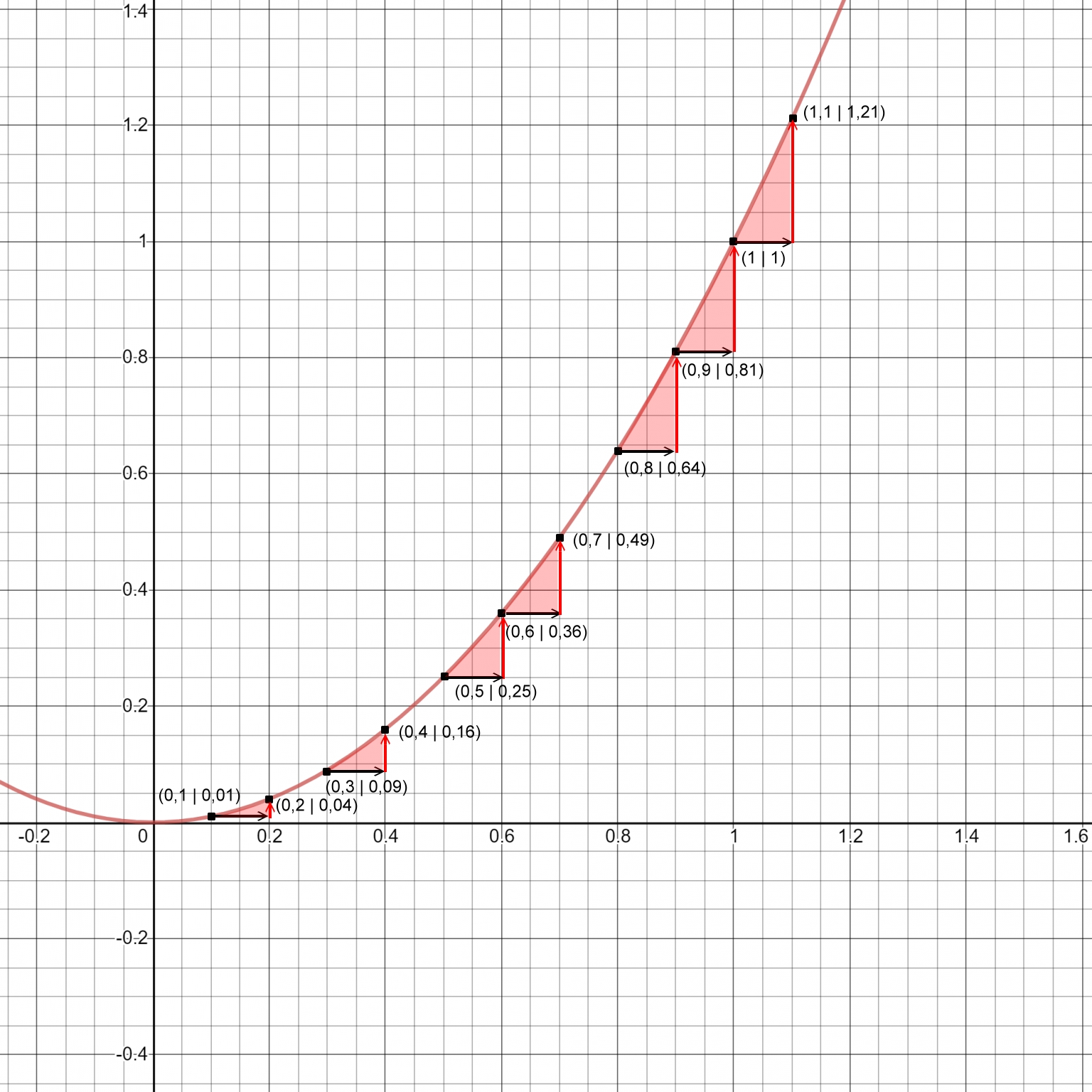
Das Intervall (0;1) zeigt den nichtlinearen Verlauf der quadratischen Funktion y=x².
Hier wachsen die Argumente zuerst schneller an als die Funktionswerte. Dies kehrt sich jedoch alsbald um. Im Punkt (1|1) sind Argument und Funktionswert gleich groß. Oberhalb des Argumentes 1 nehmen dann die Funktionswerte rasant zu.
![]()