Potenzfunktionen \( y=x^n \)

Die Funktionen mit der Vorschrift y = xⁿ oder genauer y = a xⁿ + c werden als Potenzfunktionen bezeichnet.
Die Basis x ist hier die Variable(Argument) und der Exponent n ist eine ganze Zahl, die je nachdem ob sie positiv oder negativ und dabei jeweils noch gerade oder ungerade die Eigenschaften der Funktion prägen.

Die Potenzfunktionen …

haben achsensymmetrische bzw. punktsymmetrische Parabeln oder Hyperbeln als Graphen, die alle den Punkt (1|1) gemeinsam haben. Ihre charakteristischen Verläufe machen sie gut erkennbar und unterscheidbar.

y =a xⁿ +c
Der Koeffizient a ist für Streckung, Stauchung und Spiegelung an der x-Achse verantwortlich und der
Summand c beeinflusst die Verschiebung des Graphen der Funktion auf der y-Achse.

Wir unterscheiden 4 Unterarten der Potenzfunktionen:

n ist positiv und gerade	n ist positiv und ungerade	n ist negativ und gerade	n ist negativ und ungerade
\( y = x^2 \) oder \( y = x^4 \)	\( y = x^3 \) oder \( y = x^5\)	\( y = x^{-2} \) oder \( y = x^{-4} \)	\( y = x^{-1} \) oder \( y = x^{-3}\)
Die Graphen sind achsensymmetrische Parabeln. Die Funktionen haben die Punkte (-1|1) , (0|0) und (1|1) gemeinsam. Die Nullstelle ist (0|0).	Die Graphen sind punktsymmetrische Parabeln. Die Funktionen haben die Punkte (-1|-1) , (0|0) und (1|1) gemeinsam. Die Nullstelle ist (0|0).	Die Graphen sind achsensymmetrische Hyperbeln. Die Funktionen haben die Punkte (-1|1) und (1|1) gemeinsam. Eine Nullstelle existiert nicht.	Die Graphen sind punktsymmetrische Hyperbeln. Die Funktionen haben die Punkte (-1|-1) und (1|1) gemeinsam. Eine Nullstelle existiert nicht.
Die Monotonie wechselt am Scheitelpunkt. Für negative Argumente x∈ (-∞;0)fallend. Für positive Argumente x∈ (0;∞) steigend.	Für alle Argumente x ist die Funktion monoton steigend .	Die Monotonie wechselt an der y-Achse. Für negative Argumente x∈ (-∞;0) monoton steigend. Für positive Argumente x∈ (0;∞) monoton fallend.	Für alle Argumente x mit x ≠ 0 sind diese Funktionen monoton fallend.

Nun zur grundsätzlichen Arbeit im Einzelnen:

Bei der Erforschung der Eigenschaften der Potenzfunktionen sollte man mit gut abgestimmten Wertetabellen arbeiten, um dieses Funktionen genau zeichnen zu können.

y-Werte (Funktionswerte)

...entstehen durch das Potenzieren mit dem entsprechenden Exponenten n bei \( y=x^n \).
Die zugehörigen x-Werte (Argumente) entstehen durch das Radizieren (Wurzel ziehen) mittels der n.-Wurzel für die entsprechenden Exponenten für \( y=x^n \) .

Achtung! Beim Radizieren gerader Exponenten y= x², \( y=x^4 \) usw. entstehen 2 Argumente x. \( \sqrt[4] 625 = \pm 5 \)

Allgemein gilt :
Die n.-Wurzel aus einer Zahl x ( \( \sqrt[n] x \) ) ist die Zahl y die n-mal mit sich multipliziert wieder die Zahl x (den Radikanten) ergibt.
\( \sqrt[n] x = y \) , wenn \( \underbrace{y \cdot y \cdot y … \cdot y}_{n { – mal}} \) = x

Beispiele:

\( \sqrt[3] 125 = 5 \) , denn \( \underbrace{5 \cdot 5 \cdot 5}_{3 { – mal}} \) = 125

\( \sqrt[4] 16 = 2 \) , denn \( \underbrace{2 \cdot 2 \cdot 2 \cdot 2}_{4 { – mal}} \) = 16 aber auch \( \sqrt[4] 16 = -2 \) , denn \( \underbrace{(-2) \cdot (-2) \cdot (-2) \cdot (-2)}_{4 { – mal}} \) = 16

man schreibt kurz: \( \sqrt[4] 16 = \pm 2 \)

Wir untersuchen die Funktion y = x²

Wertetabelle für y = x² im Intervall (-3; 3) Schrittweite 0,5:

Durch das Potenzieren mit 2 , auch Quadrieren genannt, (x *x =x² ) werden alle Funktionswerte y positiviert.

Wir untersuchen die Funktion y = x³

Wertetabelle für y = x³ im Intervall (-3; 3) Schrittweite 0,5:

Durch das Potenzieren mit 3 (x *x*x =x³ ) behalten die Funktionswerte y das Vorzeichen des Argumentes x.

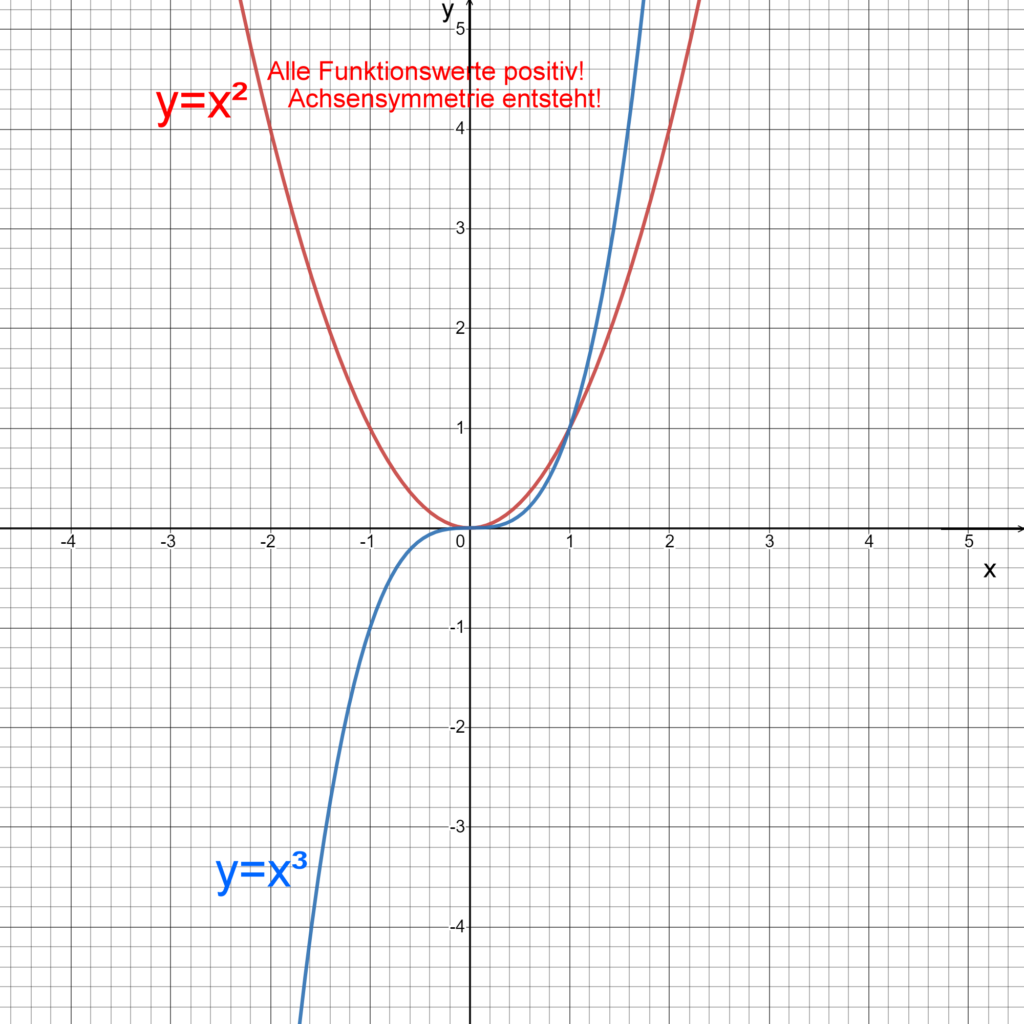
Weitere Vergleiche von Untergruppen:

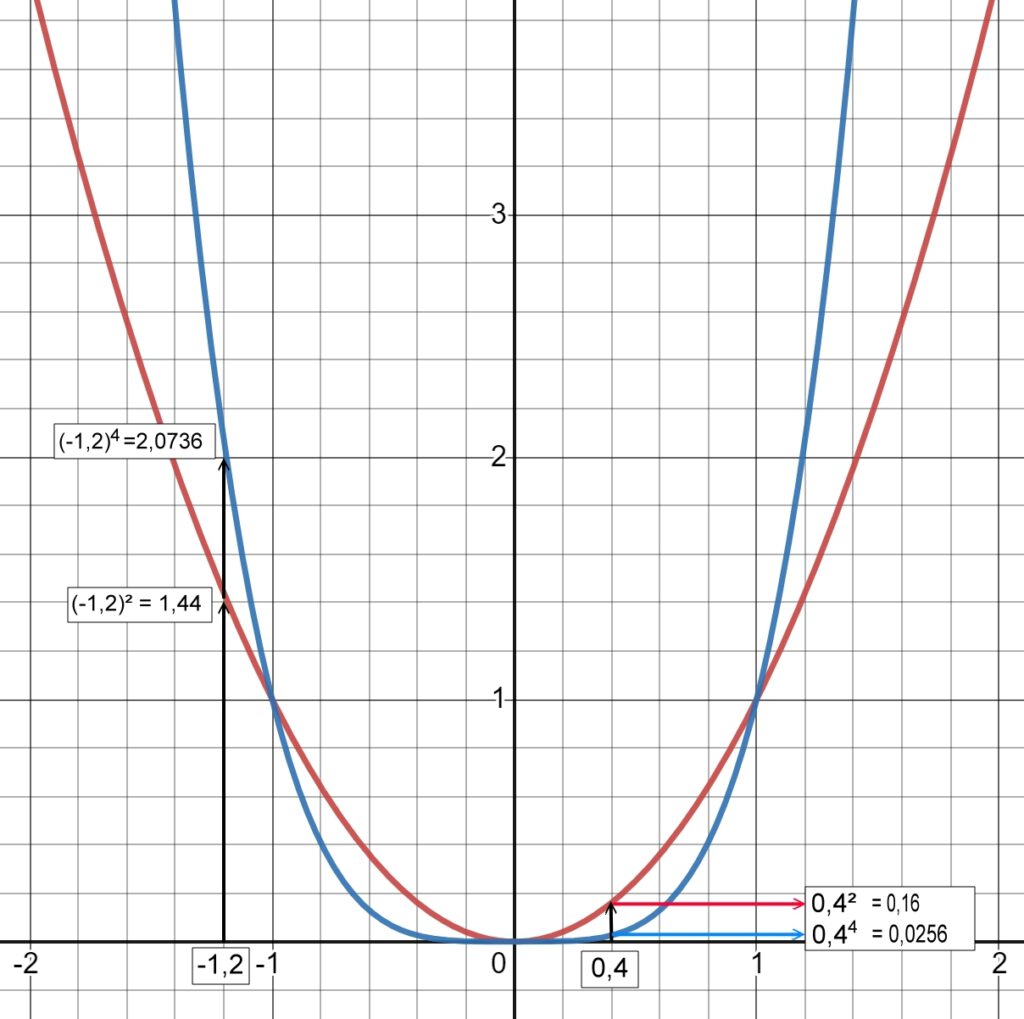
Vergleicht man die Funktionen y=x² und y = \(x^4\), so stellt man fast, dass diese Funktionen zur selben Unterklasse gehören, jedoch kleine Unterschiede im Verlauf der Graphen sichtbar sind, die durch das Potenzieren der Argumente x verursacht werden.

Beispiel Quadrieren:

2² =4 aber 0,2² = 0,04

Quadrate von Zahlen größer als 1 sind größer als ihre Argumente.
5 < 5² =25 oder 12 < 12² =144
ABER:
Der Wert 0,2 – zwischen 0 und 1 gelegen – wird beim Potenzieren kleiner als das Argument.
0,2 > 0,2² =0,04 oder 0,05 > 0,05² = 0,0025

Für \(x^4\) ist dieser Effekt noch extremer!
Hier gilt:
2 < \(2^4\) = 16 ABER : 0,2 > \(0,2^4\) = 0,016

Dieser Effekt zeigt sich im Graph deutlich!

Hier findest du eine gute Zusammenfassung zu den 4 Unterarten im Video!