Dreiecke (Quiz)

![]()
Mathe muss man üben!


![]()

![]()

Statistik kann benutzt werden um Dinge zu verkaufen, Meinung zu beeinflussen und das Denken und Tun zu manipulieren.
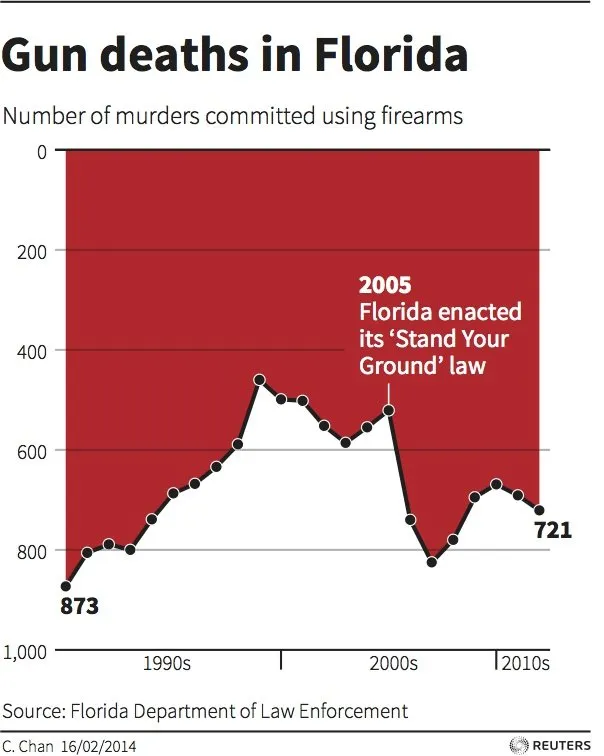
Dieses Diagramm sollte der amerikanischen Bevölkerung die Notwendigkeit eines „Stay your ground- law“, also ein Gesetz zur Verteidigung des eigenen Bodens mittels Waffen plausibel machen …
Gefunden auf :
„https://thesocietypages.org/socimages/2014/12/28/how-to-lie-with-statistics-stand-your-ground-and-gun-deaths/“
„Das Diagramm zählt die Zahl der Waffentoten in Florida. Die Linie steigt an, springt ein wenig, erreicht einen zweithöchsten Gipfel mit der Aufschrift „2005 erließ Florida sein „Stand Your Ground-law‘“ und fällt dann steil ab.
Was siehst du hier?
Die meisten Menschen sehen einen enormen Rückgang der Zahl der Schusswaffentoten, nachdem Stand Your Ground verabschiedet wurde. Aber das zeigt die Grafik nicht. Ein kurzer Blick auf die vertikale Achse zeigt, dass die Schusswechsel von oben (0) nach unten (800) gezählt werden. Die höchsten Gipfel sind die wenigsten Waffentoten und die niedrigsten die meisten. Mit anderen Worten, ein Anstieg der Linie zeigt eine Verringerung der Todesfälle durch Schusswaffen. Das Diagramm auf der rechten Seite – sowohl horizontal als auch vertikal gespiegelt – ist für die meisten intuitiver: Eine ansteigende Linie spiegelt einen Anstieg der Zahl der Schusswaffentoten wider und eine fallende.
Die richtige Schlussfolgerung ist also, dass die Zahl der Todesfälle durch Schusswaffen nach der Verabschiedung von Stand Your Ground sprunghaft angestiegen ist.
Fazit:
Dieses Beispiel ist eine großartige Erinnerung daran, dass wir unsere eigenen Annahmen in unsere Lektüre jeder Illustration von Daten einbringen. Das ursprüngliche Diagramm hat möglicherweise gegen die Konvention verstoßen, was das intuitive Lesen des Bildes falsch macht, aber die Daten sind vermutlich solide. Es liegt daher in unserer Verantwortung, bei der Aufnahme von Informationen stets unsere gebührende Sorgfalt walten zu lassen. Die Alternative ist, betrogen zu werden.“
Im folgenden Video wird das Diagramm ebenfalls besprochen …
Passend zum Thema empfehle ich die Beschäftigung mit einer Präsentation von hichert.com! LINK
Diagramme gestalten und Fehler vermeiden
Falls mal mehr Zeit ist …
![]()

Körper sind Teile des Raumes, die durch Flächen begrenzt werden . Uff, Mathematik pur.
Die Volumeneinheiten geben diesen Raum in den 3 Dimensionen an. Sie tragen den Exponenten 3 ..also m³, cm³ oder km³.
Für die Umrechnung der Volumeneinheiten gilt die Umrechnungszahl 10³ =1.000

Anleitung zum Umrechnen:
![]()