Apps für den Mathematik-Unterricht
Leider nicht immer Werbefrei!
![]()
Der Sinussatz

Erklärung im Selbstversuch…
- Zeichne ein beliebiges Dreieck und miss seine Seiten und die 3 Innenwinkel.
- Bilde nun jeweils die Quotienten $$\frac{Seite} {sin(zugehöriger Winkel)} $$
- Du solltest feststellen, dass die Quotienten gleich groß sind!
- Damit kann man diese Quotienten gleichsetzen.
- Es entstehen 3 Verhältnisgleichungen!
- Die 3 Sinussätze:
\( \frac{a}{sin \alpha} =\frac{b}{sin \beta} oder \frac{a}{sin \alpha} =\frac{c}{sin \gamma} oder \frac{b}{sin \beta} =\frac{c}{sin \gamma} \)
Es gilt:
\( \frac{a}{sin \alpha} =\frac{b}{sin \beta} oder \frac{a}{sin \alpha} =\frac{c}{sin \gamma} oder \frac{b}{sin \beta} =\frac{c}{sin \gamma} \)
„Mit 3 gegebenen Werten zu einem Dreieck, von denen 2 Werte ein Seite-Winkel-Paar darstellen, kann man eine 4. Größe errechnen und danach die restlichen beiden Größen des Dreiecks ermitteln!„
Experiment zum Sinus-Satz (Variante 2)
Tipp: Erarbeite Dir ein Beispiel einer „Seitenberechnung“ und eine Beispiel für eine „Winkelberechnung“!
Für Fortgeschrittene:
Herleitung:
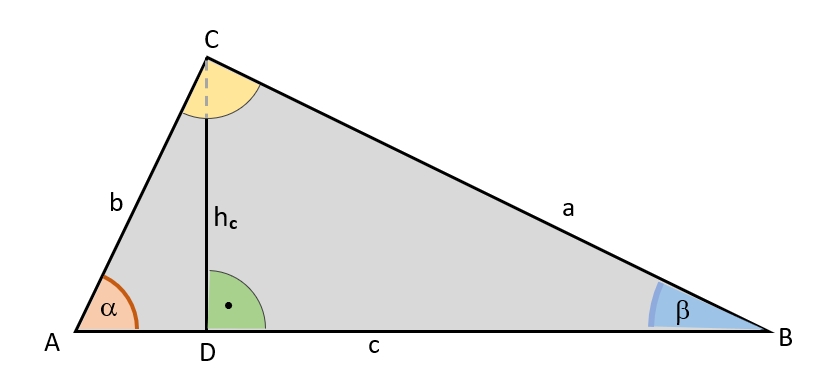
Im allgemeinen Dreieck gelten für die einbeschriebene Höhe auf Seite c (hc) die folgenden Gleichungen:
\( sin \alpha = \frac {GK}{H} = \frac {h_c}{b} \) und \( sin \beta = \frac {GK}{H} = \frac {h_c}{a} \)
Also gelten auch die umgestellten Gleichungen:
\( h_c = b \cdot sin \alpha \) und \( h_c = a \cdot sin \beta \)
Und damit gilt :
\( b \cdot sin \alpha = a \cdot sin \beta~~ \vert:sin \alpha ~~ \vert : sin \beta \)
Somit auch:
\( \frac {b} {sin \beta} = \frac {a}{ sin \alpha} \)
Wendet man das Verfahren auf die Höhe auf Seite b oder a an, gilt allgemein auch:
\( \frac {b} {sin \beta} = \frac {a}{ sin \beta} = \frac {c}{ sin \gamma}\) , der „SINUS-SATZ“ genannt.
„Mit 3 gegebenen Werten zu einem Dreieck, von denen 2 Werte ein Seite-Winkel-Paar darstellen, kann man eine 4. Größe errechnen und danach die restlichen beiden Größen des Dreiecks ermitteln!„
Beispielrechnung:
![]()
Achsensymmetrie
![]()
