Winkel am rechtwinkligen Dreieck -sin, cos, tan
Für diese Lektion solltest Du unbedingt die Umstellung von Formeln und Gleichungen beherrschen!
Im Dreieck liegt dem kleinsten Winkel die kürzeste Seite gegenüber.
Dem größten Winkel liegt die längste Seite gegenüber!
Im rechtwinkligen Dreieck gibt es 2 spitze Winkel.
Für diese spitzen Winkel gilt:
Ein Schenkel des Winkels ist die Hypotenuse des Dreiecks.
Der andere Schenkel wird Ankathete (AK) des Winkles genannt!
Die dem Winkel gegenüberliegende Seite ist eine Kathete. Sie wird Gegenkathete (GK) des Winkels genannt!


Für die Größen am rechtwinkligen Dreieck gelten folgende Beziehungen und Rechenvorschriften!
Wenn x ein spitzer Winkel des rechtwinkligen Dreiecks ist:

Zwei der Größen einer dieser obigen Gleichungen müssen bekannt sein,
um die dritte Größe in dieser Gleichung zu berechnen!
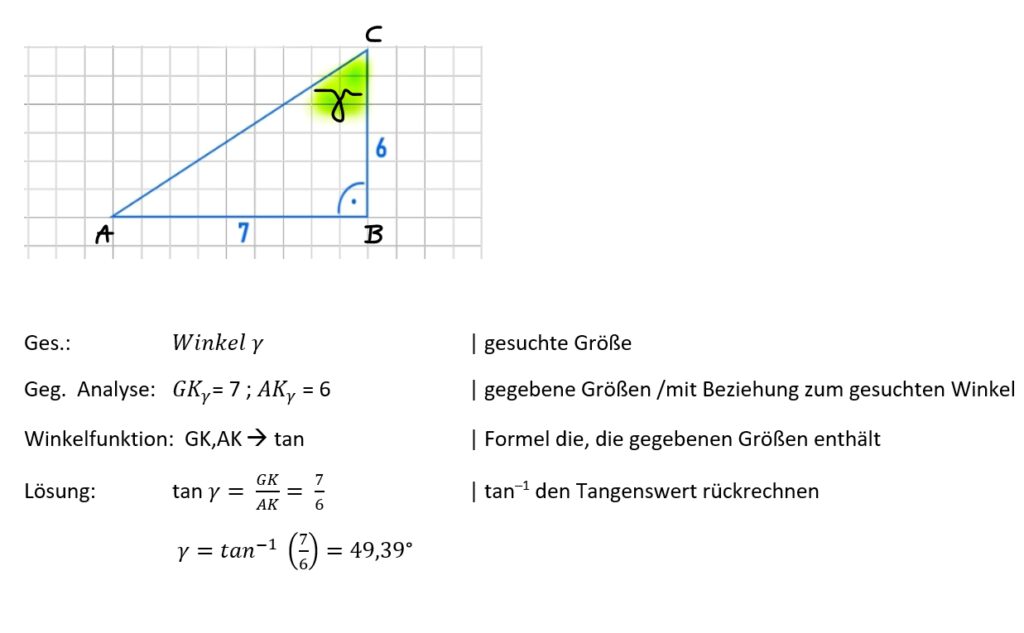
Beispiel Winkelberechnung:
![]()

