Die Sinusfunktion y=a sin (bx)
Die Funktion y = a *sin (x)
Der Faktor a bewirkt eine Vervielfachung der Funktionswerte, wie wir sie schon von anderen Funktionen her kennen.
Sein Effekt auf den Graphen nennt man Streckung für a>1 und Stauchung für 0<a< 1.
Funktionswerte verkleinern / vergrößern sich, das Maximum/ Minimum liegt dann bei a und -a und nicht mehr bei 1 und -1.
Die „Lage der Nullstellen“ und die „Länge der kleinsten Periode“ beeinflusst der Koeffizient a nicht.
Nutzt man negative Werte für a, kommt es zur Spiegelung des Graphen an der x-Achse(Abszisse).
Die Amplitude – die Ausschlaghöhe – der Funktion wird hier beeinflusst.
Probiere hier aus, wie der Koeffizient a auf den Graphen wirkt!
Quelle: Christian Bauer , geogebra.org
Die Funktion y = sin (bx)
Der Faktor b führt bei bei der Funktion zur Veränderung der kleinsten Periode.
Normalerweise beträgt sie bei y=sin(x) genau 2![]() .
.
Der Faktor b verändert diese Länge auf der x-Achse, auf der sich der Graph periodisch wiederholt.
Die Periodenlänge errechnet sich aus:
$$\frac {2* \pi}{b} $$
Das Intervall von Null bis zum Wert der kleinsten Periode sollte dann zur Zeichnung geviertelt werden, um
Maxima, Minimum und Nullstellen zu errechnen.
Untersuche den Einfluss von b auf den Graphen von y = sin (b*x)
Quelle: Christian Bauer, geogebra.org
Beide Faktoren in der Funktion y=f(x) = \( a \cdot sin(b \cdot x \) )
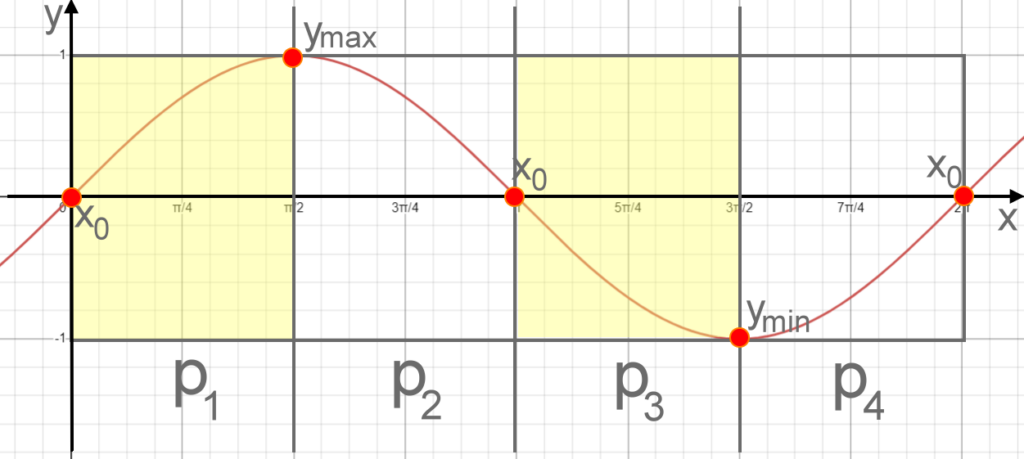
Zeichnen von Funktionen dieser Form:
- \( Notiere^{(1)} \) mit Hilfe von Faktor a die Werte \( y_{max} und y_{min} \)
- Berechne die Periodenlänge mit p = \( \frac{2 \pi}{b} \)
- Teile den Wert p durch 4 (Abschnitte der einzelnen Quadranten \( p_1 , p_2, p_3 und p_4 \) )
- Jeder Quadrant enthält am Anfang und Ende einen typischen Fixpunkt ( \( x_0 , y_{min} oder y_{max} \) )
- Abschnitt \( p_1 \) Nullstelle bis \( y_{max} , \) harmonisch zeichnen
- Abschnitt \( p_2 \) \( y_{max} , \) bis Nullstelle harmonisch zeichnen
- Abschnitt \( p_3 , \) Nullstelle bis \( y_{min} , \) harmonisch zeichnen
- Abschnitt \( p_4 \) \( y_{min} , \) bis Nullstelle harmonisch zeichnen
(1) Sollte a<0 sein, so tauschen \( y_{max} , \) und \( y_{min} , \) die Funktion
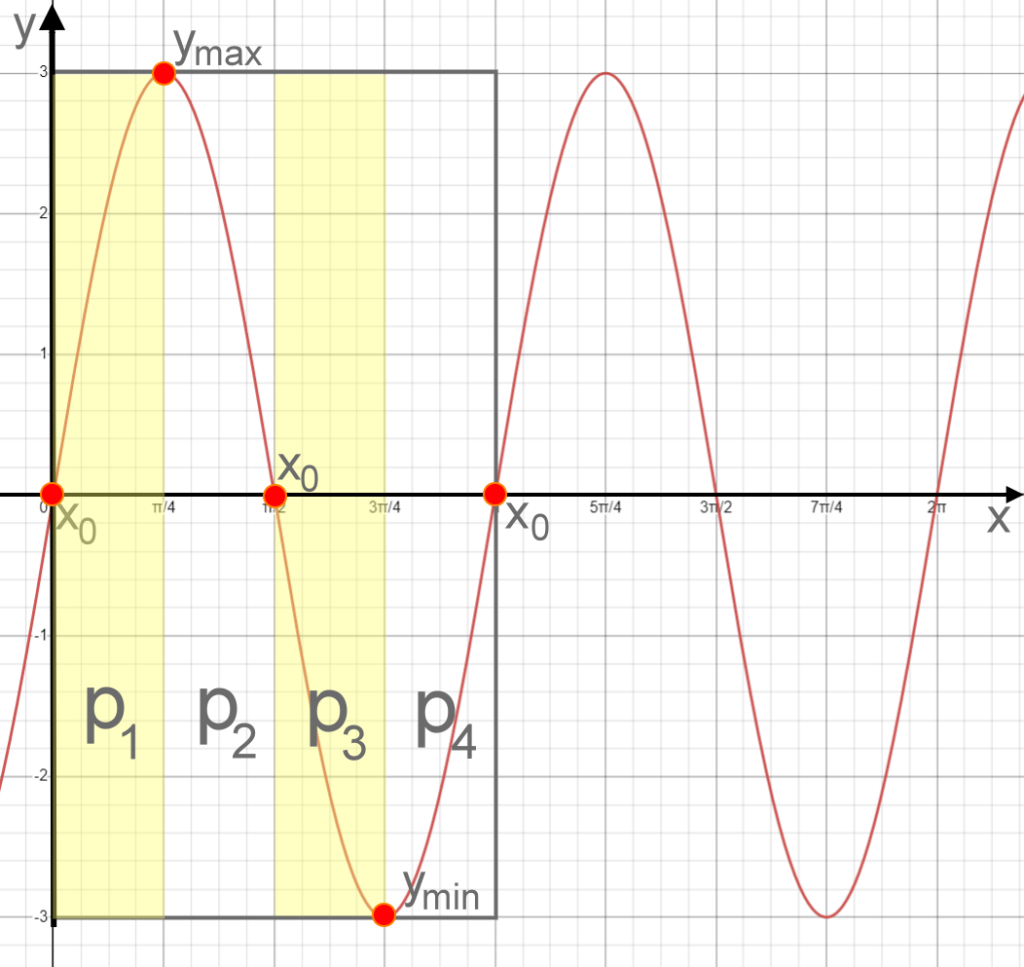
Beispiel: y=f(x) =3 sin (2x); a = 3; b = 2
- Notiere mit Hilfe von Faktor a=3 die Werte \( y_{max}=3 \) und \( y_{min}=-3 \)
- Berechne die Periodenlänge mit p = \( \frac{2 \pi}{b} \) = \( \frac{2 \pi}{2} = \pi \)
- Teile den Wert p=\( \pi \) durch 4 ( jeder Abschnitt ist also \( p_{(1,2,3,4)}= \frac{\pi}{4} \) lang )
- Jeder Quadrant enthält am Anfang und Ende einen typischen Fixpunkt ( \( x_0 , y_{min} \) oder \( y_{max} \) )
- Abschnitt \( p_1 \) von 0 bis \( \frac{\pi}{4} \) ; Nullstelle \( x_0 \)=0 bis \( y_{max} , \) =3 harmonisch zeichnen
- Abschnitt \( p_2 \) von \( \frac{\pi}{4} \) bis 2 \( \frac{\pi}{4} \) =\( \frac{\pi}{2} \)) ; \( y_{max} =3, \) bis Nullstelle \(x_0=0 \)harmonisch zeichnen
- Abschnitt \( p_3 \) von \( \frac{\pi}{2} \) bis 3 \( \frac{\pi}{4} \) =\( \frac{3 \cdot \pi}{4} \)) ;Nullstelle \( x_0 \)=0 bis \( y_{min} , \) = – 3 harmonisch zeichnen
- Abschnitt \( p_4 \) von \( \frac{ 3 \cdot \pi}{4} \) bis 4 \( \frac{\pi}{4} \) = \( \pi \) ; \( y_{min} \) = – 3 bis Nullstelle \( x_0 \) = 0 harmonisch zeichnen
Eventuell sollten bei großen Werten für a oder b auch Wertetabellen zum Einsatz kommen, die das harmonische Zeichnen mit Zwischenwerten unterstützen.
Die Funktion y=f(x)=a sin (bx) + c (mit Physik – Fachsprache)
![]()



 /3
/3