Körper und Netze – Memory

![]()
Mathe muss man üben!


![]()

![]()
Zu den Langzeitkrediten, die über Jahre laufen gibt es auch Kurzzeitgeschäfte, bei denen Geld nur für Tage oder Monate angelegt oder verliehen wird. Im Prinzip ist es auch möglich, Geld nur für einen Tag anzulegen.
Die Zinsen für solche Geschäfte errechnen sich aus den Monats- und Tageszinsformeln:
m- Anzahl der Monate
i- Anzahl der Tage
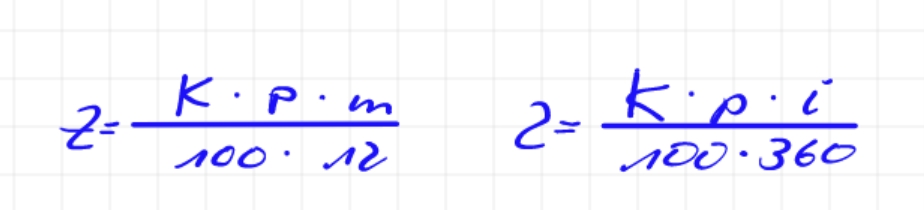
Allerdings gibt es eine Vereinbarung zu beachten:
Das Bankenjahr hat 12 Monate mit jeweils 30 Tagen!
Jeder Monat wird mit 30 Zinstagen berechnet!
Wird in einer Aufgabe also angegeben, über wie viele Tage oder Monate ein Geldgeschäft abgeschlossen wird, so benutzt man die obigen Formeln!
Hier die Erklärung von Lehrer Schmidt und ein paar Beispielaufgaben dazu:
![]()

Auflösung und Angebote zur weiteren Übung und Erklärung
![]()